Problems of time

One reason “path integral quantum gravity canonical quantum gravity” is regarding problems of time. Several problems of time that trouble canonical approaches are absent in path integral approaches. Sorkin¹ has given a quite insightful discussion on the topic, which I summarize below.

Two understandings of quantum theory

Sorkin distinguishes two understand quantum theory: the framework vs. the sum-over-histories framework. In the framework,

the essence of quantum mechanics resides in its mathematical structure: a Hilbert space, an algebra of operators to be interpreted physically in terms of measurements; and a “projection postulate”, which tells us how to take the results of measurements into account in predicting probabilities for future measurements. […] Closely allied with the Ψ-framework is the canonical quantization approach to quantum gravity. Although different variants of this approach may employ different combinations of the basic dynamical variables, they all work solely with space (in the sense of a spacelike hypersurface), as opposed to spacetime.

While in the sum-over-histories framework,

the spacetime history itself is the central object. It exists in the same sense in which a history is taken to exist in classical physics, and the physical interpretation can thus be made directly in terms of properties of this history […] Since the sum-over-histories is by nature a “spacetime approach”, it naturally leads to a version of quantum gravity which works with spacetime as opposed to data on a hypersurface.

Problems of time for the 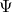framework

Sorkin highlights three problems of time for the framework. The first has to do with “logical ordering” for projection operators:

In employing that postulate [projection postulate], one writes the projections in a definite sequence determined by the order of the observations in time; but how can such a rule avoid leading to a vicious circle in a theory in which time itself is one of the things being “observed”?

The second has to do with “frozen formalism” of canonical quantization of gravity:

In consequence of the Hamiltonian constraints, the “physical observables” are necessarily all time-independent (they are what Karel Kuchar [27] calls ‘perennials’), and one seems forced into an attempt to “fix the time-gauge” in order to recover a semblance of spacetime from the disembodied spacelike hypersurface to which the formalism directly refers. Not only is such a procedure technically questionable, but it can be dangerous as well: one can easily smuggle arbitrary answers to important physical questions into the theory in the guise of a “gauge choice”, for example to the question whether collapse to a singularity is inevitable in “mini-superspace cosmology”.

The third has to do with the early universe:

Finally, in a framework based on “observables” rather than “beables”, how are we to speak about (say) the early universe, if there were no observers then and none in the offing for a long time to come? Since some of the most important applications of quantum gravity are likely to be precisely to the early universe, this also appears to present a serious difficulty.

No such problems in the sum-over-histories framework

According to Sorkin, the above problems of time are absent in the sum-over-histories framework:

None of these “problems of time” would seem to exist for the sum-over-histories/spacetime approach. Time itself doesn’t need to be recovered, because it is there from the very beginning as an aspect of the spacetime metric. The projection postulate is irrelevant, because there is no state-vector to be “reduced”. And the early universe existed just as much as we ourselves do here and now, even if from our vantage point it is relatively remote and inaccessible.

Discussions

Not everyone agrees with this assessment. For instance, in their discussion about problems of time in quantum cosmology, Kiefer and Peter² hold that:

[…] The discussion presented here is based on the canonical (Hamiltonian) formalism of quantum GR. Alternatively, one can use the covariant (path-integral) formulation. At the formal level, that is, neglecting field-theoretic subtleties, the two formulations are equivalent: the path integral satisfies the Wheeler–DeWitt equation and the momentum constraints ([4], Section 5.3.4). For this reason, all issues related to the problem of time hold equally well in the covariant formulation.

I believe the last statement misses some crucial qualifications, which will be discussed in another post. Once the qualifications are added, it is fair to say that issues related to the problem of time DO NOT hold equally well in the covariant formulation.

1. Sorkin (1997) “Forks in the road, on the way to quantum gravity”, arXiv:gr-qc/9706002. ↩︎
2. Kiefer & Peter (2022) “Time in quantum cosmology“, arXiv:2112.05788. ↩︎