Description
Title: Who’s afraid of infinite action?
Author: Ding Jia
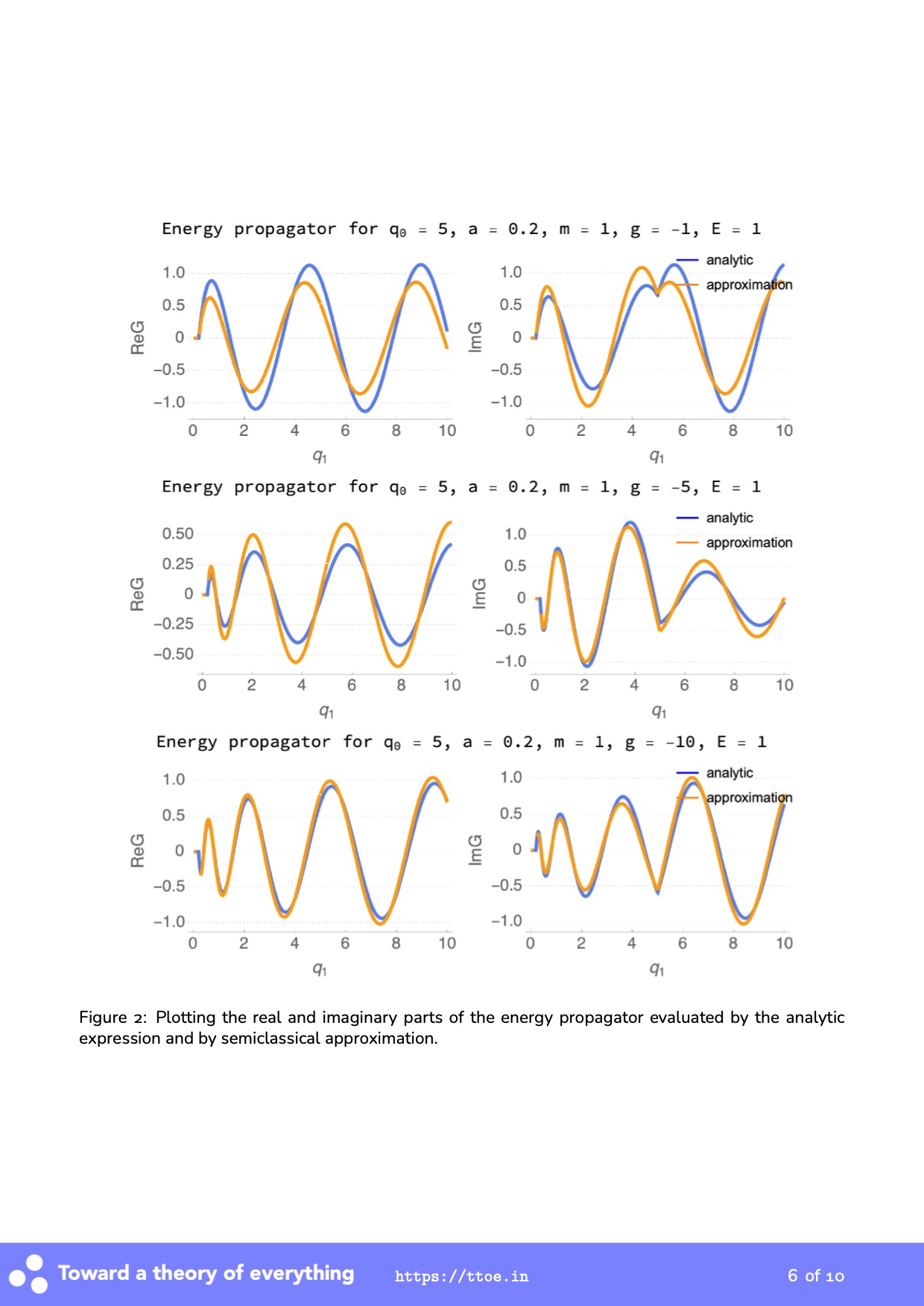
Abstract: Dynamical solutions can generically be derived from the Euler-Lagrange equation for stationary action. However, not all solutions are associated with finite action. In recent years, several authors proposed to drop such solutions because they give ill-defined quantum amplitudes or lead to destructive interference in path integrals. Here I challenge this position with a counterexample. For a quantum particle in a strongly attractive inverse square potential, a bouncing solution is needed in an accurate semiclassical saddle point approximation for the energy propagator. Although the solution has infinite action, a limit exists to give well-defined contributions. Therefore infinite-action solutions cannot be discarded in general.
This product contains an article in .pdf format. The purchase includes all future versions of the article.
Version history
- Original versions: Article v1.0










Reviews
There are no reviews yet.